sintesi di reti sequenziali

1. descrizione verbale
2. automa della macchina sequenziale
3. automa della rete (codifiche binarie)
4. tavola degli stati futuri
5. espressioni booleane delle funzioni di eccitazione e uscite
6. disegno della rete

N.B.: Occorre un passo di minimizzazione dell’automa a stati finiti.

N.B.: Le espressioni booleane minimali servono per la realizzazione con porte logiche o programmable logic array (PLA), invece se si usa la read only memory (ROM) o i multiplexer (MUX) non serve eplicitare le espressioni booleane.

esempio

1. descrizione verbale

Circuito che riceve in ingresso $x$ e produce in uscita 1 se riconosce 1101 con sovrapposizioni.

2. stati dell’automa

$S_{in}$: stato iniziale $S_1$: riconoscimento del primo bit $S_{11}$: riconosciuto due bit

	0	1
$S_{in}$	$S_{in}/0$	$S_1/0$
$S_1$	$S_{in}/0$	$S_{11}/0$
$S_{11}$	$S_{110}/0$	$S_{11}/0$
$S_{110}$	$S_{in}/0$	$S_1/1$
Quest’automa è minimo, cioè è costruito con meno stati possibili? Si, perché non ci sono [[criterio di minimalità	stati equivalenti]].

3. codifica degli stati

• Input: gli input sono già codificati.
• Stati: In tutto ci sono 4 stati, quindi ci servono 2 bit.

	$y_1$	$y_0$
$S_0$	0	0
$S_1$	0	1
$S_{11}$	1	0
$S_{110}$	1	1
Scritto ciò, la tabella degli stati dell’automa al passaggio 1 può essere riscritta come:

	0	1
$00$	00/0	01/0
$01$	00/0	10/0
$10$	11/0	10/0
$11$	00/0	01/1

• Output: gli output sono già codificati.

4. tavola degli stati futuri

$x$ (input)	$y_1$	$y_0$		$Y_1$	$Y_0$		$z$ (output)
0	0	0		0	0		0
0	0	1		0	0		0
0	1	0		1	1		0
0	1	1		0	0		0
1	0	0		0	1		0
1	0	1		1	0		0
1	1	0		1	0		0
1	1	1		0	1		1

realizzazione con i flip-flop JK

$x$	$y_1$	$y_0$		$Y_1$	$Y_0$		$z$		$j_1,k_1$	$j_0,k_0$
0	0	0		0	0		0		0 $\delta$	0 $\delta$
0	0	1		0	0		0		0 $\delta$	$\delta$ 1
0	1	0		1	1		0		$\delta$ 0	1 $\delta$
0	1	1		0	0		0		$\delta$ 1	$\delta$ 1
1	0	0		0	1		0		0 $\delta$	1 $\delta$
1	0	1		1	0		0		1 $\delta$	$\delta$ 1
1	1	0		1	0		0		$\delta$ 0	0 $\delta$
1	1	1		0	1		1		$\delta$ 1	$\delta$ 0

5JK. espressioni booleane

• $z$ è di immediato riconoscimento: $z=x{y}_1{y}_0$

$x$ \ $y_1{y}_0$	00	01	11	10
0	0	0	$\delta$	$\delta$
1	0	1	$\delta$	$\delta$
$j_1=x{y}_0$

$x$ \ $y_1{y}_0$	00	01	11	10
0	$\delta$	$\delta$	1	0
1	$\delta$	$\delta$	1	0
$k_1=y_0$

$x$ \ $y_1{y}_0$	00	01	11	10
0	0	$\delta$	$\delta$	1
1	1	$\delta$	$\delta$	0
$j_0=\overline{x}{y}_1+x\overline{y_1}=x\oplus y_1$

$x$ \ $y_1{y}_0$	00	01	11	10
0	$\delta$	1	1	$\delta$
1	$\delta$	1	0	$\delta$
$k_0=\overline{x}+\overline{y_1}$

6JK. disegno della rete

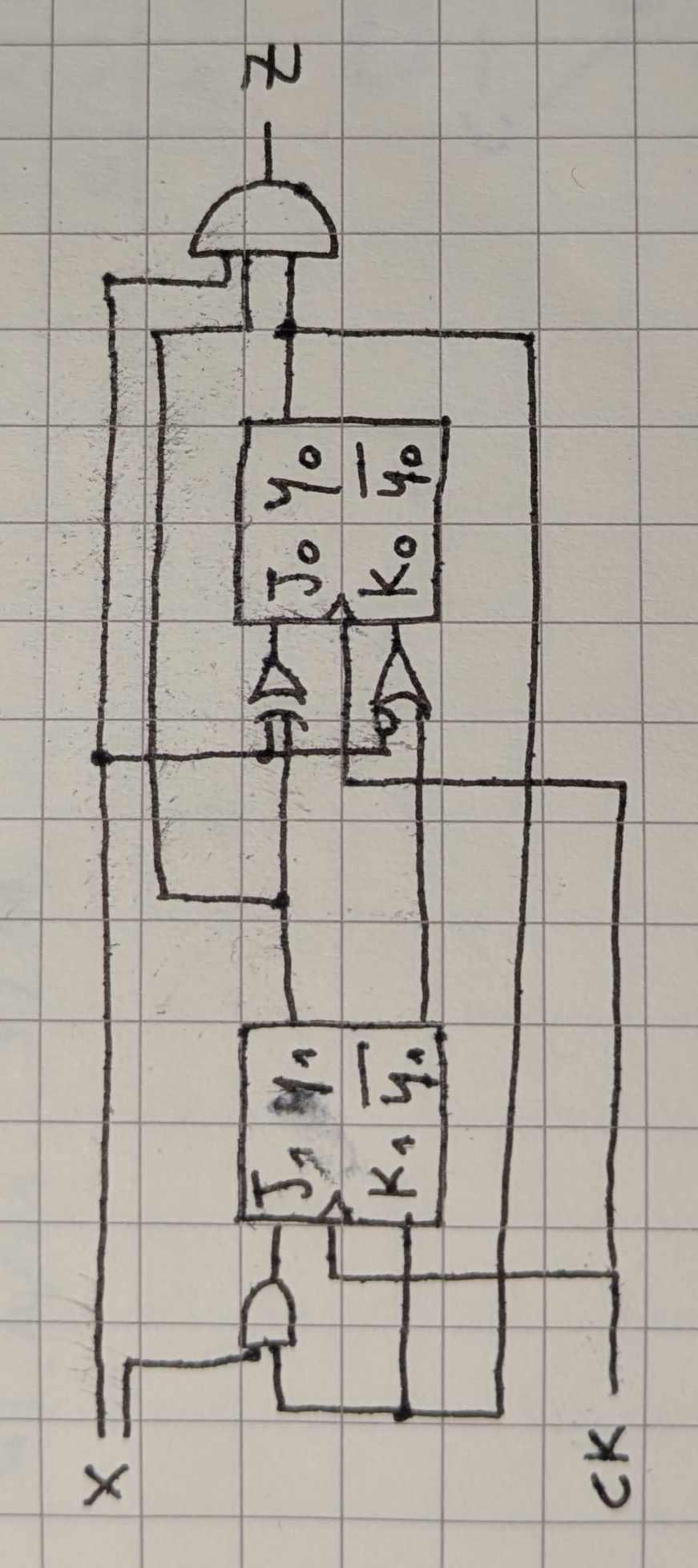
realizzazione con i flip-flop D

Ora realizziamo la stessa rete ma con i flip flop D (più semplice)

4D. tavola degli stati futuri

$x$	$y_1$	$y_0$		$Y_1$	$Y_0$		$z$		$d_1,d_0$
0	0	0		0	0		0		0 0
0	0	1		0	0		0		0 0
0	1	0		1	1		0		1 1
0	1	1		0	0		0		0 0
1	0	0		0	1		0		0 1
1	0	1		1	0		0		1 0
1	1	0		1	0		0		1 0
1	1	1		0	1		1		0 1

5D. espressioni booleane

• $z$ è di immediato riconoscimento: $z=x{y}_1{y}_0$

• $d_1$

$x$ \ $y_1{y}_0$	00	01	11	10
0	0	0	0	1
1	0	1	0	1

• $d_0$

$x$ \ $y_1{y}_0$	00	01	11	10
0	0	0	0	1
1	0	1	0	1

realizzazione con i flip-flop JK combinati alla ROM

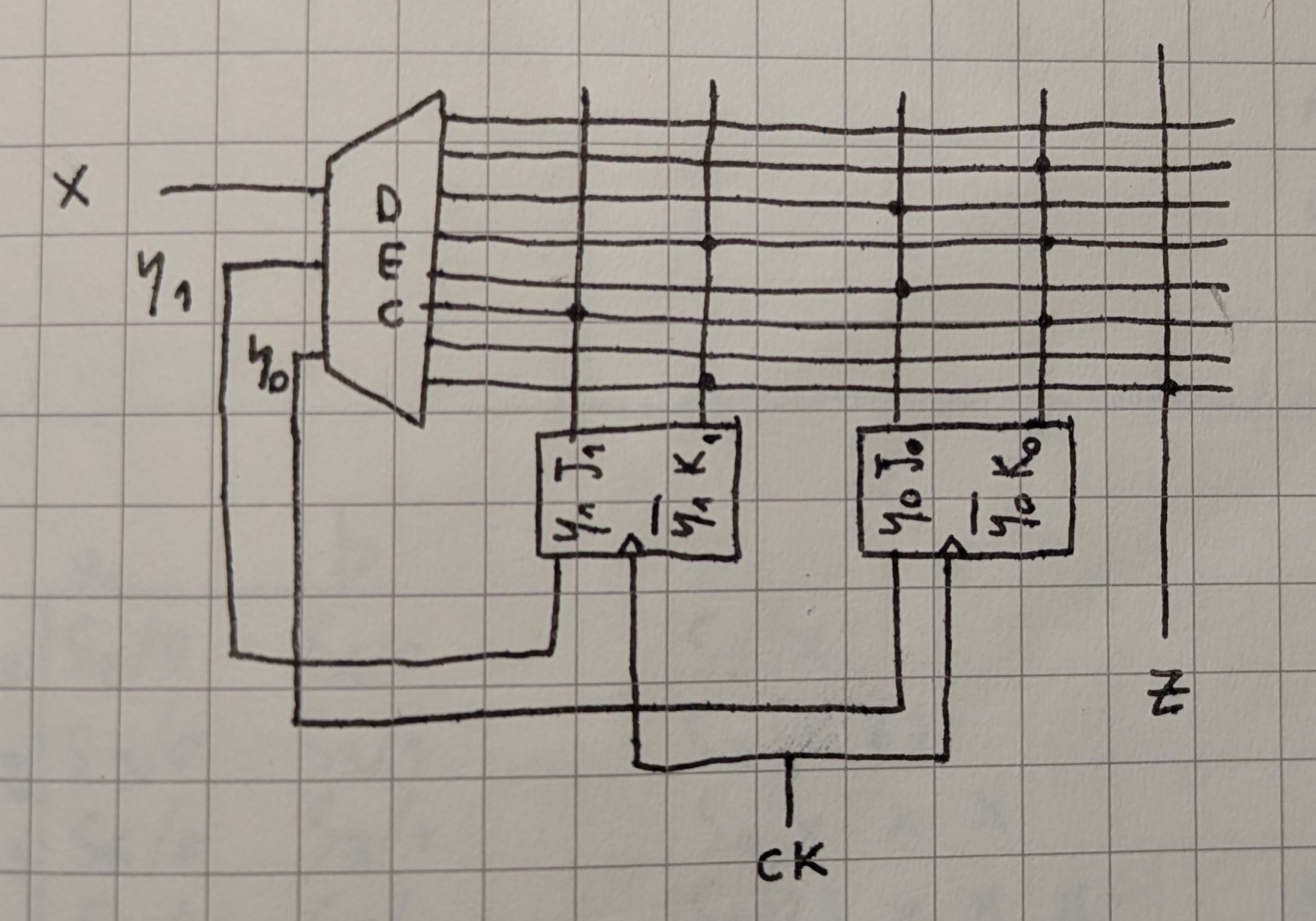
N.B.: Il vantaggio è che non vanno ricavate le espressioni booleane perché i valori degli output possono essere codificati direttamente nella ROM.