automa a stati finiti (finite state automata)

modelli di automa

modello di Mealy

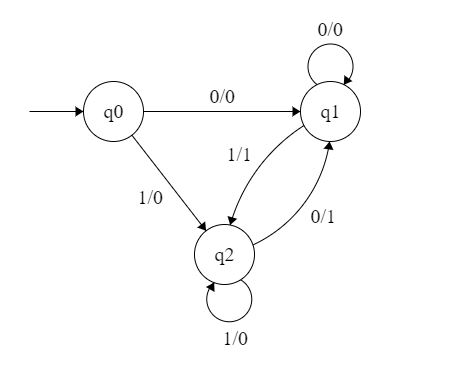
secondo il modello di Mealy, l’automa a stati finiti è la struttura matematica che ha:

• $\Sigma$: un’alfabeto finito di ingresso in cui sono scritti gli input

• $Q$: un’insieme finito di stati che può assumere la memoria (rappresentati nel diagramma dal contenuto dei cerchi)

• $\delta$: è la funzione di transizione $\delta :\Sigma \times Q\to Q$ (rappresentate nel diagramma come gli archi tra i cerchi). Il suo dominio è $\Sigma \times Q$ e il suo codominio è $Q$. Esempio: (0, 01) → 01

• $U$ è l’alfabeto finito di uscita

• $\lambda$ è la funzione di uscita $\lambda :\Sigma \times Q\to U$

Esempio di macchina di Mealy (foto da geeksforgeeks.org)

modello di Moore

Differisce dal modello di Mealy solo per la funzione di uscita $\lambda$, qui definita come ${\lambda }^{\prime }:Q\to U$

Nel modello di Moore, l’uscita prodotta dallo stato dell’automa + lo stato dell’automa stesso sono considerati come un singolo stato.

Esempio di macchina di Moore (foto da geeksforgeeks.org)

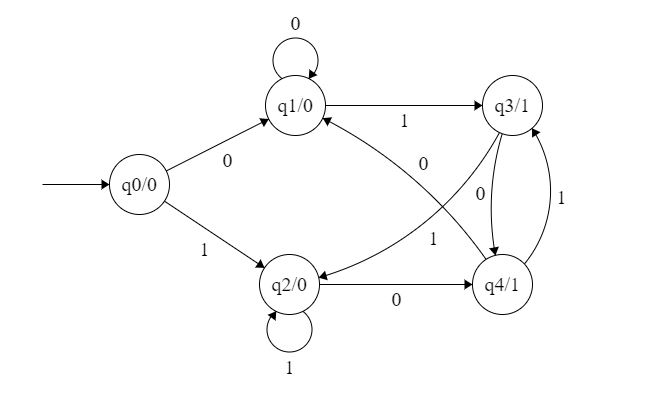
tabella dell’automa

Una tavola degli stati futuri può essere rappresentata come tabella dell’automa, le cui caselle rappresentano lo stato futuro dell’automa a partire dallo stato (sulla riga) avendo un’input (sulla colonna).

stati / input	0	1
$S_I$	$S_I/0$	$S_1/0$
$S_1$	$S_{10}/0$	$S_{11}/0$
$S_2$	$S_I/0$	$S_1/1$
$S_3$	$S_{10}/0$	$S_{11}/0$

• esempio di progettazione dell’automa della macchina distributrice

Automa dei linguaggi regolari

Delle regex (espressioni regolari) di un linguaggio regolare possono essere riconosciute e prodotte da un automa a stati finiti secondo le regole del linguaggio. C’è un teorema di equivalenza che stabilisce un parallelismo tra automi a stati finiti e definizioni di linguaggi regolari.