Un’applicazione lineare, anche detta trasformazione lineare, è un omomorfismo tra spazi vettoriali (definiti sullo stesso campo) che preserva le combinazioni lineari.
N.B.: un’applicazione lineare biiettiva è un isomorfismo tra spazi vettoriali.
Formalmente, dati gli spazi vettoriali e definiti sul campo , si dice applicazione lineare se gode delle proprietà di:
- additività:
- omogeneità di grado 1:
Equivalentemente, le due proprietà possono essere combinate nel principio di sovrapposizione, cioè la preservazione delle combinazioni lineari:
L’applicazione è detta endomorfismo di ; se è biiettiva (), viene chiamata automorfismo di .
Osservazione: un’applicazione lineare iniettiva manda sottoinsiemi del dominio di vettori linearmente indipendenti in sottoinsiemi del codominio linearmente indipendenti.
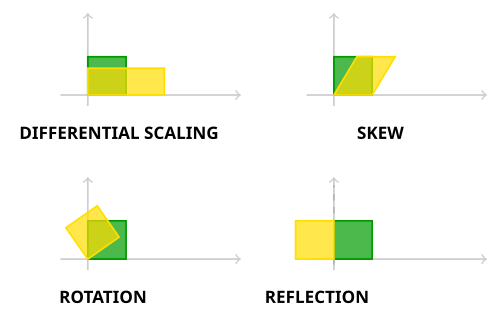
Esempi di applicazioni/trasformazioni lineari in :
Matrice associata
Dato che la trasformazione lineare trasforma allo stesso modo tutti i vettori, è utile descriverla come “azione” sui vettori di una base qualsiasi del dominio, in particolare della sua base canonica.
La matrice associata si costruisce mettendo uno dopo l’altro da sinistra a destra i risultati di applicata ai vettori della base canonica, uno alla volta.
Ad esempio la trasformazione in da , la cui base canonica è :
a la cui base è :
si scrive .
La prima colonna mappa il vettore unità sull’asse (cioè ) al vettore , mentre la seconda colonna mappa il vettore unità sull’asse (cioè ) al vettore . Dato che tutti i vettori in sono combinazioni lineari dei vettori della base canonica, e tutti i vettori in sono combinazioni lineari di , la trasformazione è completamente rappresentabile come la matrice associata.
Infatti vale che:
N.B: l’immagine di è un sottospazio vettoriale di .
Kernel
Il Kernel, o nucleo di è l’insieme , cioè l’insieme di vettori di che, se trasformati da , puntano all’origine di . Per definizione è un sottospazio vettoriale di .
Per trovare il kernel di un’applicazione lineare, basta trovare i vettori che puntano allo zero di risolvendo il sistema di equazioni lineari , dove e è la matrice associata.
Ad esempio, in con :
Quindi (il sottospazio vettoriale triviale): solo punta all’origine di .
Teorema della dimensione
Se e hanno dimensione finita, vale che:
N.B.: Ciò può essere usato come un criterio per scoprire se una trasformazione è lineare.