permutazioni

Formalmente, una permutazione può essere vista come una mappa mappa biiettiva tra due collezioni ordinate che contengono gli stessi elementi in ordine diverso o uguale (permutazione banale).

Notazioni

Notazione compatta

$$\tau =(cabd)$$

Assumendo che gli elementi dell’insieme da permutare sono gli stessi permutati da $\tau$, cioè $\{a,b,c,d\}$, il primo elemento di $\tau$ indica che il primo elemento in ordine alfabetico ($a$) deve essere mappato a $c$, il secondo ($b$) a $a$, il terzo ($c$) a $b$ e l’ultimo ($d$) a $d$.

N.B.: Ovviamente gli elementi permutati devono avere un ordine naturale per poter usare questa notazione.

Notazione di Cauchy

$$\tau =\left(\begin{array}{c}abcd\\ cabd\end{array}\right)$$

Ogni elemento della riga superiore mappa al suo elemento sottostante.

Invertire una permutazione è banale, basta invertire le righe:

$${\tau }^{-1}=\left(\begin{array}{c}cabd\\ abcd\end{array}\right)$$

e opzionalmente riordinare le colonne in ordine alfabetico rispetto alla riga superiore:

$${\tau }^{-1}=\left(\begin{array}{c}abcd\\ bcad\end{array}\right)$$

Notazione ciclica

Oppure in notazione ciclica, la permutazione sopra di può scrivere $(acb)(d)$, perché $a$ mappa a $c$, $c$ mappa a $b$, $b$ mappa ad $a$ e il ciclo si ripete, mentre $d$ rimane invariato: quindi si scrivono le due “isole” (cicli a supporto disgiunto) $a\to c\to b\to a$ e $d\to d$ separatamente. $(d)$ si può ignorare perché è un invariante.

La notazione ciclica ci permette di applicare la permutazione a un determinato elemento dell’insieme che permuta, scrivendo la permutazione a sinistra e l’argomento tra parentesi tonde a destra.

$$(acb)\left(a\right)=c$$ $$(acb)\left(b\right)=a$$ $$(acb)\left(c\right)=b$$ $$(acb)\left(d\right)=d$$

N.B.: PIÙ PERMUTAZIONI SUCCESSIVE SI APPLICANO DA DESTRA A SINISTRA.

N.B.: Ogni trasposizione può essere scomposta unicamente in più cicli disgiunti, ma anche non unicamente in più 2-cicli non necessariamente disgiunti, anche detti trasposizioni.

Permutazione ciclica

È una permutazione che consiste in un singolo ciclo; tutti gli altri elementi permutati rimangono invariati.

Esempio:

$$\rho =\left(\begin{array}{c}12345\\ 13245\end{array}\right)=(1)(23)(4)(5)=(23)$$

I cicli possono essere prefissati dalla loro lunghezza, in questo caso $\rho$ è un 2-ciclo o $(\star \text{ꙮ}\text{🥀})$ è un 3-ciclo.

Due cicli (o permutazioni cicliche) si dicono supporti disgiunti se non hanno elementi in comune, formando due “isole” separate, ad esempio $(ab)(cde)$.

I 2-cicli si chiamano anche trasposizioni.

Gli 1-cicli sono evidentemente invarianti.

Glossario

Parità

Si dice parità di una permutazione la parità del numero di cicli disgiunti in cui può essere scomposta (0 = numero pari di cicli disgiunti, 1 = numero dispari).

La parità può anche essere dedotta “disegnando” la permutazione.

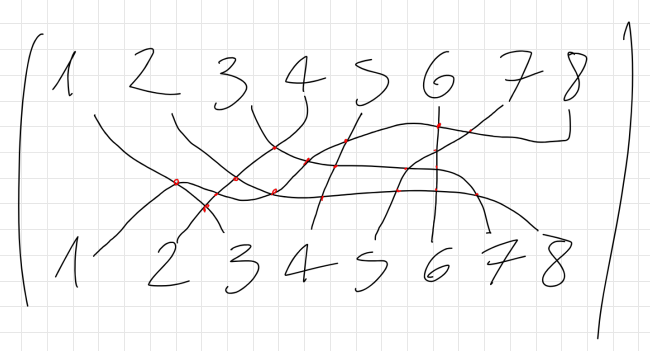
In questo caso le “trasposizioni” si incrociano in 18 punti: 18 è un numero pari quindi la parità è 0.

Segnatura

$\epsilon (\sigma )$ si dice segnatura di una permutazione: è una funzione che restituisce:

• $-1$, se $\sigma$ è un $n-$ciclo con $n$ pari;
• $gr1$, se $\sigma$ è un $n-$ciclo con $n$ dispari;
• il prodotto delle segnature dei cicli a supporti disgiunti in cui si può scomporre $\sigma$, se $\sigma$ non è un $n-$ciclo.

Ordine

Dato $\sigma \in S_n$ l’ordine di $\sigma$ è il più piccolo $m\ge 0$ tale che ${\sigma }^m={\text{Id}}_{S_n}$. Se $\sigma$ è il prodotto di cicli disgiunti allora $m$ è il (mcm) minimo comune multiplo delle lunghezze dei cicli.

Quante sono le permutazioni di un insieme con cardinalità $n$?

$$n\cdot (n-1)\cdot (n-2)\cdot \dots \cdot 2\cdot 1=n!$$

N.B.: Per definizione, $0!=1$

Esempio: quante parole di lunghezza 8 posso formare con i caratteri V E R O N I C A? $8!$

Osservazione: e se invece se avessimo caratteri ripetuti come in M O N D O? Qui avremmo $\frac{5!}{2!}$ parole diverse di lunghezza 5, perché abbiamo contato ogni parola 2 volte distinguendo erroneamente le O, quindi dobbiamo eliminare tutti i modi diversi di ordinare le due O, cioè $2!$ (2). Questo è un esempio di disposizione senza ripetizione.