full adder (FA)

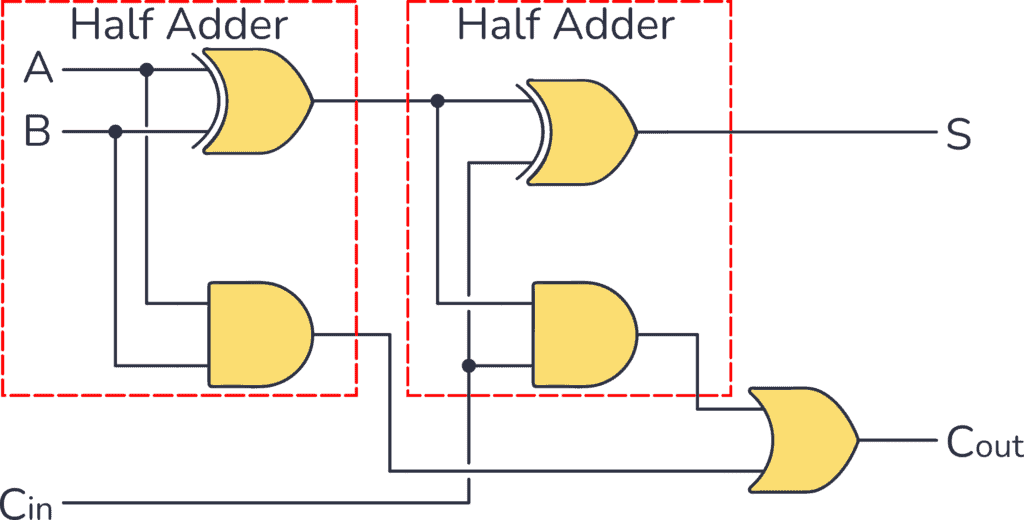
Si ottiene concatenando 2 half adder (HA).

a	b	c (riporto in entrata)	s (somma)	r (riporto)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1
$s=\overline{a}(b\oplus c)+a(\overline{b\oplus c})=a\oplus (b\oplus c)$ (per la definizione stessa di XOR)
$r=\overline{a}bc+a(b+c)$

mappa di Karnaugh del riporto/resto in uscita ($r$):

a sotto / bc a destra	00	01	11	10
0	0	0	1	0
1	0	1	1	1
Gli implicanti della SOP sono 101-111, 011-111, 111-110

$r=ac+ab+bc=ab+c(a+b)$: questa è l’espressione minimale del riporto; ma dato che nel circuito abbiamo già uno XOR (quello del risultato della somma), possiamo trovare un modo di riusarlo per diminuire le porte logiche necessarie per creare il circuito completo.

Stranamente $r=ab+c(a\oplus b)$ è equivalente all’espressione di partenza $r=ab+c(a+b)$, ciò si può verificare con l’induzione perfetta.