Some times ago, while designing a custom CPU emulator, I stumbled into a math problem: I needed to pick random whole numbers in any given range using only a (boolean) value that can casually become 0 or 1 if asked.

Think of this random, two-sided value as a coin that can be tossed on its head (1) or tail (0), and imagine ranges from 0 to n as an n+1 sided dice.

This simplification works because extracting a casual number from 20 to 25 can be thought as extracting it from 0 to 5 and adding a fixed offset, like 20 in this case.

First attempt, summing coin tosses

Let's try to simulate a classic six sided dice. Could we toss 5 coins and take the number of heads +1 to get numbers from 1 to 6?

I tested this approach with one million "dice" made like this and this is the result:

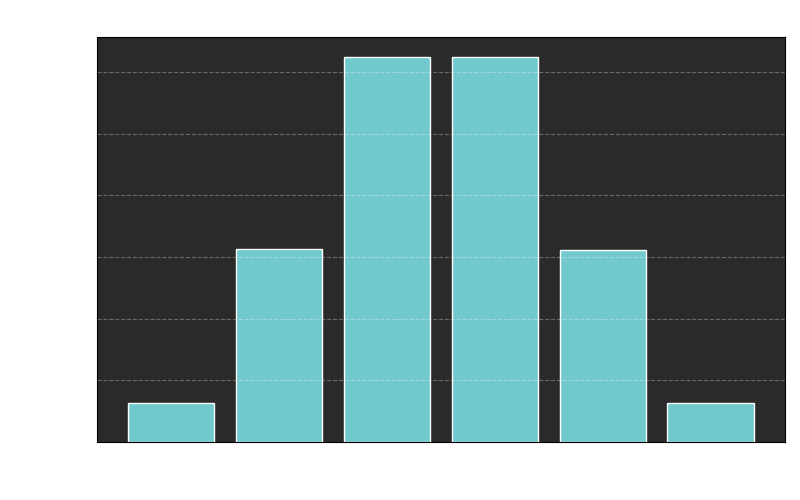
Clearly the distribution of outcomes is uneven (and it can be proven to be binomial). We should have expected this because if we toss 5 coins, according to the rule we chose, there happens to be:

• only one way to get 1 (all heads),
• 5 ways to get 2 (every combination with 1 head and 4 tails),
• 10 ways to get 3 (every combination with 2 heads and 3 tails),
• 10 ways to get 4 (every combination with 3 heads and 2 tails),
• 5 ways to get 5 (every combination with 4 head and 1 tails),
• only one way to get 6 (all tails).

Another approach, coin tosses as choices

If a coin toss is a casual fair choice between heads or tails (2 possible states), how can we extend this perfect fairness to more possible states, so more possible numbers?

Suppose we need to pick a number between 0 and 7 (8 sided dice). The idea is simple, we can chain choices like this:

       1°       first toss, we choose either [0,1,2,3] or [4,5,6,7] 
      / \
     /   \
    /     \
   2°      2°   second toss, we can choose [0,1] or [2,3], [4, 5] or [6, 7]  
  / \     / \
 3°  3°  3°  3° third toss, we choose 0 or 1, 2 or 3, 4 or 5, 6 or 7
/ \ / \ / \ / \
0 1 2 3 4 5 6 7 (final states)

This is a binary tree, because we start from the initial range, then we can branch left or right at every step in our path, finally reaching a number.

A path in a binary tree is equivalent to a number written in binary, because 0 can be thought as right and 1 as left, so we can treat coin tosses as binary digits to get a random number.

With this very efficient process we halve the number of choices left to make every time we make one (logarithmic growth of choices as the number of final states grows).

There's a problem

As it is, we can only have dices whose number of faces is a power of two, but the initial request deals with any possible range.

To simulate a 6 sided dice, we can toss 3 coins like before, as 2^3 (8) is the smallest power of two larger than 6, but we need a way to adapt the range [0; 7] to the range [0; 5].

Wrapping numbers around a wheel?

To solve the problem quickly, we could map the range [0; 2^n] to our desired range.

The modulo operator (%) appears to fit the job nicely, because it "wraps" the infinite number line into a finite wheel. Think of it like a 12 hours clock marking the infinite passing of hours.

Concretely, here's how the mapping is done:

0 1 2 3 4 5 6 7  [0; 8] range
| | | | | | | |  n % 6
0 1 2 3 4 5 0 1  [0; 6] range

Despite being a quick fix, this approach is biased, because 2 numbers map to 0, another 2 map to 1, but only one number each maps to 2, 3, 4 and 5, so 0 and 1 will be more probable than other numbers.

Rejection sampling

What if we gave up and just discard the numbers outside our desired range, then try again until we get a valid number?

Actually, there's no way around it without increasing the amount of coins used or having a biased distribution.

It's trivial to prove that in the worst case, the number of dice rolls rejected tends to 50%, but how bad would this be?

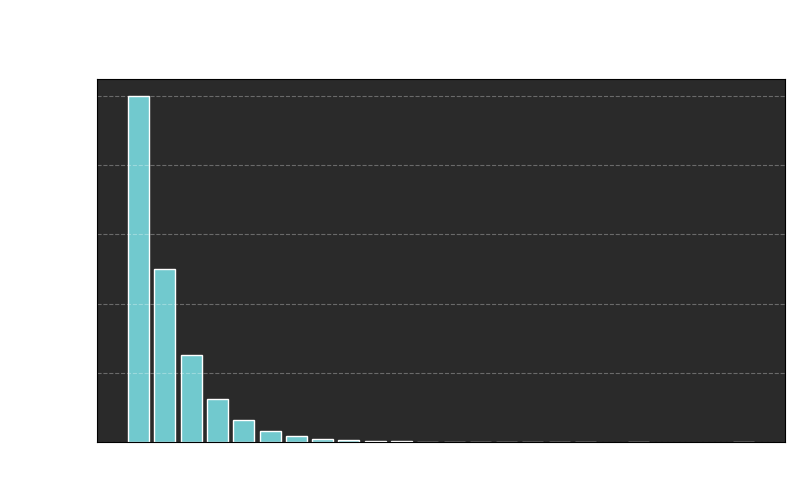
This isn’t as bad as it looked on paper: in a million dice rolls, 99% of rolls produced a valid number after 6 retries or fewer, 90% within 3 retries, and 50% after just 1 retry.

This shows that the method is not only elegant and fair, but also unexpectedly efficient.