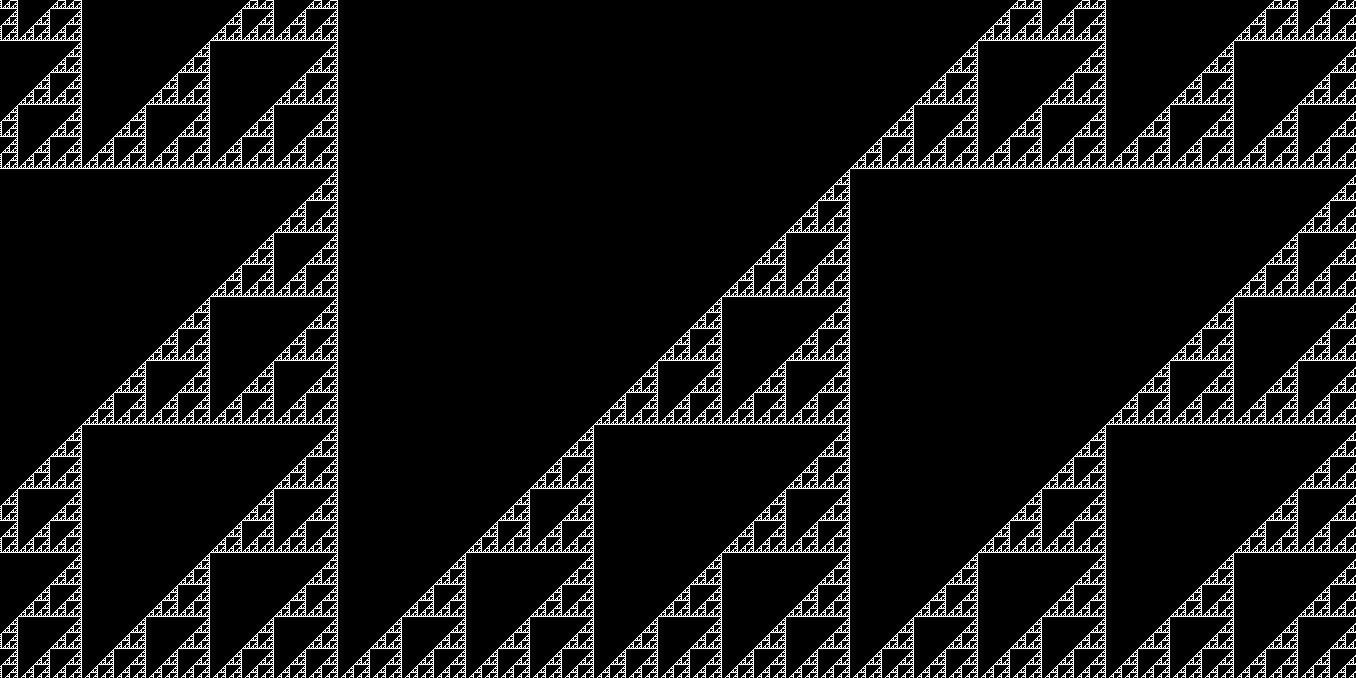^ generated with rule 102 automaton

What is a cellular automaton?

A cellular automaton is a collection of cells, usually arranged in a grid (2D automata) or a line (1D automata), where cells change state (0 or 1) all at once, following a simple specified rule set based on the state of neighbouring cells.

A complex self replicating system emerges from simple rules.

The concept of cellular automata was developed by the mathematicians, physicists and computer scientists John von Neumann and Stanislaw Ulam in the 1940s while working on the atomic bomb at Los Alamos, then it was expanded further in the 1970s by the work of John Conway, who invented the famous Conway's Game of Life (see the GIF above) which you can try here, and by Stephen Wolfram in the 1980s.

Naive implementation of 1D automata

Every automaton can be implemented easily with the same process, but let's say that we want to implement the rule 102 one.

First of all, what does rule 102 even mean? It's a rule set that considers every possible situation in which a cell could be in a moment and computes its next state.

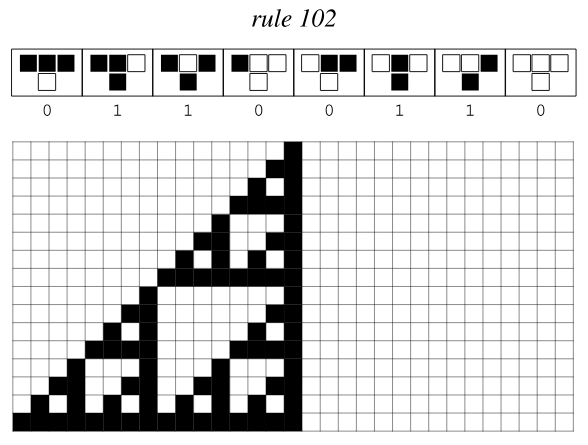
Let's see: for every cell in the line we can say that a cell and its left/right neighbours can be either 0 or 1, so there are 2^3 = 8 possible combinations of these three. Every combination can result in the cell changing its state to 0 or 1, so we can start writing a truth table, considering the current states of left/central/right cells as inputs, and the next state of the central as the output.

L = left cell
C = central cell
R = right cell
C' = C next state

L C R | C'
0 0 0 | ?
0 0 1 | ?
0 1 0 | ?
0 1 1 | ?
1 0 0 | ?
1 0 1 | ?
1 1 0 | ?
1 1 1 | ?

102 is simply a compact way to express every output (C') mapped to every input configuration (L C R): in binary 102 is 01100110, so we write it in the truth table from top to bottom.

L C R | C'
0 0 0 | 0
0 0 1 | 1
0 1 0 | 1
0 1 1 | 0
1 0 0 | 0
1 0 1 | 1
1 1 0 | 1
1 1 1 | 0

To make a naive implementation in our programming language of choice, we could:

1. Loop on every cell of the current line
   1. get its left-right-center configuration and the output mapped to it on our look-up table,
   2. insert the new computed state inside of new line's corresponding position.
2. Print the new line and consider it as the current one, repeat the process until reaching the desired number of iterations.

This process has complexity O(n^2) because we iterate for n lines on n cells (considering a square grid).

Is there a cleaner, better way to do it?

Of course!

Notice that we apply the same rule set to every cell in the current line, so there must be a way to apply it all at once, provided that we find:

• a way to encode the rule set with boolean logic,
• the array of right neighbours of every cell (spoiler: we won't need the array of left ones)

Transforming the table into a logic operation

Notice that the output is 1 if and only if the central cell and the right neighbour cell are in a different state; the left neighbour cell doesn't play a role. This is, by definition, the logic operation of exclusive or (XOR) between right and central cell.

Note: we found by chance an exceptional rule set that reduces to a simple logic operator, but even if the majority of rule are not that simple to reduce, they can still be expressed by a logic expression, made out of multiple operators.

Right neighbouring cells

The array of right neighbours of every cell can be made by shifting the line of cells to the left by one position.

New algorithm

Now we have every ingredient to get from computing the single cells to computing whole rows instantly:

1. print the current line,
2. shift the current row of cells by one to the left,
3. set the current row to (itself XOR itself shifted by one to the left)
4. repeat until reaching the desired number of iterations.

The complexity went from O(n^2) to O(n), isn't that amazing?

Python Implementation

cells = 1 # initial configuration = 0000...001
for i in range(64): # repeat 65 times
    print("{:064b}".format(cells)) # print cell row (64 bits) in binary
    cells = cells ^ (cells << 1)

output: 

00000000000000000000000000000001
00000000000000000000000000000011
00000000000000000000000000000101
00000000000000000000000000001111
00000000000000000000000000010001
00000000000000000000000000110011
00000000000000000000000001010101
00000000000000000000000011111111
00000000000000000000000100000001
00000000000000000000001100000011
00000000000000000000010100000101
00000000000000000000111100001111
00000000000000000001000100010001
00000000000000000011001100110011
00000000000000000101010101010101
00000000000000001111111111111111
00000000000000010000000000000001
00000000000000110000000000000011
00000000000001010000000000000101
00000000000011110000000000001111
00000000000100010000000000010001
00000000001100110000000000110011
00000000010101010000000001010101
00000000111111110000000011111111
00000001000000010000000100000001
00000011000000110000001100000011
00000101000001010000010100000101
00001111000011110000111100001111
00010001000100010001000100010001
00110011001100110011001100110011
01010101010101010101010101010101
11111111111111111111111111111111